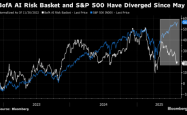
深入浅出解析三元二次方程：数学中的璀璨明珠

11 阅读：3 2025-08-09 20:20:29 评论：0

在数学的广阔天地中，方程式犹如璀璨的明珠，照亮了无数求解者的道路。而在这其中，三元二次方程更是以其独特的魅力和复杂性，吸引了无数数学爱好者的目光。那么，什么是三元二次方程？它有哪些特点？我们又该如何求解它呢？下面，就让我们一起来揭开三元二次方程的神秘面纱。

### 什么是三元二次方程？

三元二次方程，顾名思义，是指含有三个未知数，且未知数的最高次数为2的方程。它的一般形式可以表示为：

\[ ax^2 + bx + c = 0 \]

\[ dy^2 + ey + f = 0 \]

\[ gz^2 + hz + i = 0 \]

其中，\(a, b, c, d, e, f, g, h, i\) 为常数，且 \(a, d, g \neq 0\)。

### 三元二次方程的特点

1. 复杂性：由于三元二次方程含有三个未知数，因此求解过程相对复杂，需要运用多种数学方法和技巧。

2. 多样性：三元二次方程的形式多样，可能存在实根、复根或无根的情况，这使得求解过程更加富有挑战性。

3. 应用广泛：三元二次方程在物理学、工程学、经济学等领域都有广泛的应用，例如求解物体运动轨迹、电路分析、经济预测等。

### 如何求解三元二次方程？

求解三元二次方程，通常有以下几种方法：

1. 因式分解法：将方程中的三个二次多项式分别因式分解，然后根据因式分解的结果求解未知数。

2. 配方法：通过配方将方程转化为标准形式，然后利用求根公式求解未知数。

3. 换元法：将方程中的三个未知数进行换元，将原方程转化为二元二次方程，然后求解。

4. 数值法：利用计算机或数值计算软件，通过迭代法求解方程。

### 实例分析

以下是一个三元二次方程的实例：

\[ x^2 + y^2 + z^2 - 2xy - 4xz + 2yz = 0 \]

我们可以通过因式分解法来求解此方程。首先，将方程中的三个二次多项式分别因式分解：

\[ (x - y - 2z)(x + y - z) = 0 \]

然后，根据因式分解的结果，我们可以得到以下三个方程：

\[ x - y - 2z = 0 \]

\[ x + y - z = 0 \]

\[ x^2 + y^2 + z^2 - 2xy - 4xz + 2yz = 0 \]

接下来，我们可以分别求解这三个方程，得到方程的解。

### 总结

三元二次方程是数学中的一个重要分支，它具有复杂性、多样性和广泛的应用。掌握求解三元二次方程的方法，有助于我们更好地理解数学，并在实际生活中解决各种问题。让我们在数学的海洋中，继续探索，发现更多美丽的方程式吧！